Approximating square roots with Newton's method
Newton’s method is a way to approximate the roots of an equation. The idea is to start with an initial guess, then to approximate the function by its tangent line, and finally to compute the x-intercept of the tangent line. The x-intercept is a better approximation of the root than the initial guess, and the process can be repeated until the desired accuracy is reached.
Let’s say we need to find the square root of a number a. The equation we need to solve is \(f(x) = x^2 - a = 0\).
-
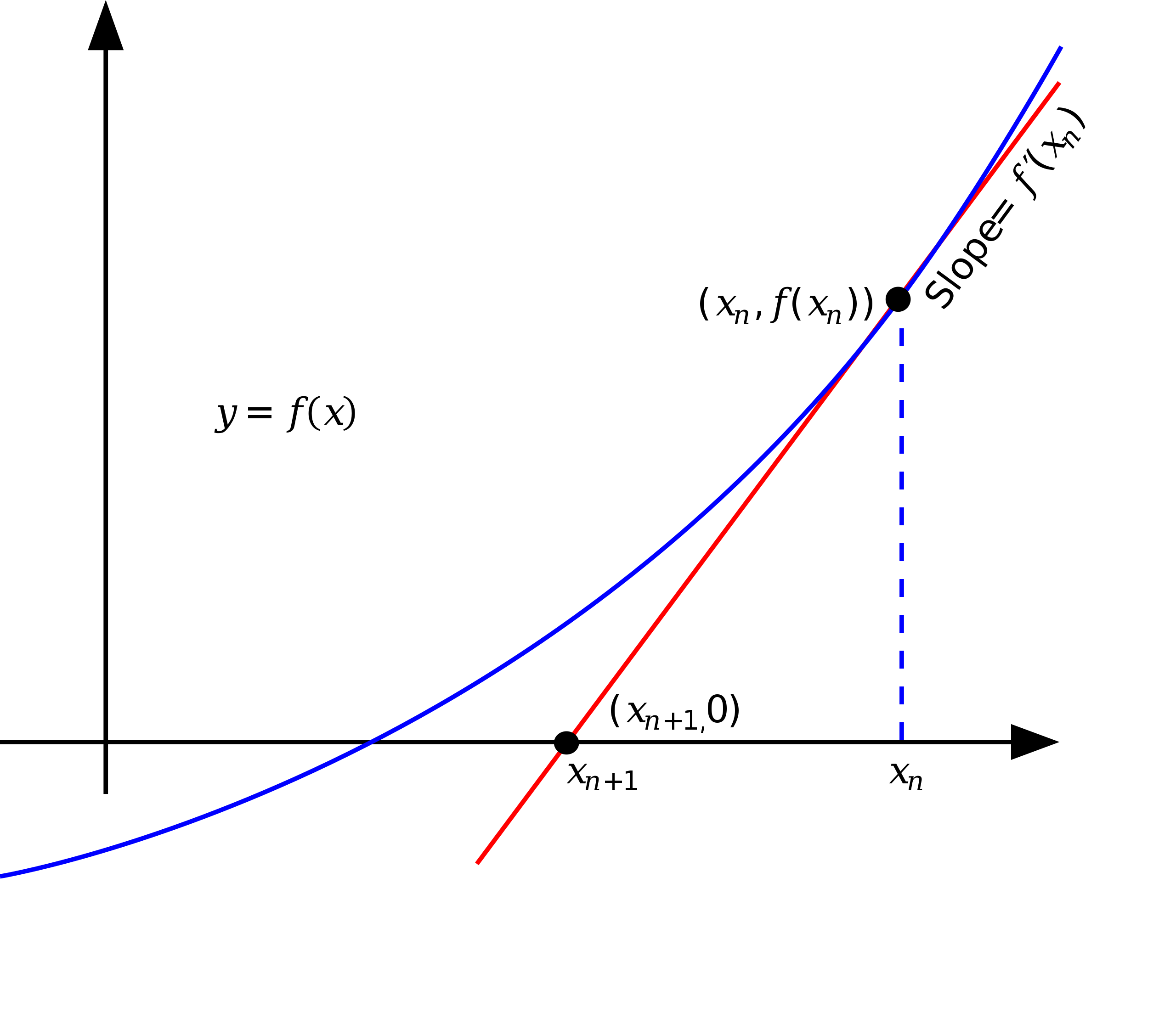
We can start by drawing the curve of the function \(f(x)\) (Blue line in the figure below). The curve is a parabola ,but it shows only one root, the positive root.
-
Then, we can start by choosing an initial guess \(x_n\) (Blue dashed line in the figure below). The tangent line at the point \(x_n\) is \(f'(x_n) = 2x_n\) (Red line in the figure below). The x-intercept of the tangent line is the next guess.
-
As you can see, the next guess \(x_{n+1}\) is closer to the root than the previous guess \(x_n\). The process can be repeated until the desired accuracy is reached.
So, we can approximate the square root of \(a\) by:
\[x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\] \[= x_n - \frac{x_n^2 - a}{2x_n}\] \[= \frac{1}{2} (x_n + \frac{a}{x_n})\]We start with an initial guess \(x_0\) and then we iterate over the formula until we reach a desired accuracy. For each step, we can calculate the error \(\epsilon\) as:
\[\epsilon = \frac{|x_{n+1} - x_n|}{x_{n+1}}\]For example, if the first guess is \(x_0 = 1\), and the new guess is \(x_1 = 1.5\), then the error is:
\[\epsilon = \frac{|1.5 - 1|}{1.5} = 0.333\]The error value ranges between \(0\) and \(1\), and the smaller the error, the closer we are to the square root of \(a\). When the error equals \(0\), we have reached the square root of \(a\). We can also define an accepted error so that we stop iterating when the error is less than the accepted error.
Example (1)
Let’s find the square root of \(a = 9\) using Newton’s method. We start with an initial guess \(x_0 = 1\), and then we iterate over the formula until we reach a desired accuracy. This time, we will use an accepted error of \(0\). The following table shows the steps:
| \(n\) | \(x_n\) | \(x_{n+1}\) | \(\epsilon\) |
|---|---|---|---|
| 0 | 1 | 5 | 0.8 |
| 1 | 5 | 3.4 | 0.47 |
| 2 | 3.4 | 3.023 | 0.12 |
| 3 | 3.023 | 3.000091 | 0.0076 |
| 4 | 3.000091 | 3.000000092 | 0.00003 |
| 5 | 3.000000092 | 3.000000000 | 0.00000003 |
| 6 | 3 | 3 | 0 |
As we can see, after the sixth step, the error is equal to \(0\), so we have reached the square root of \(9\).
Example (2)
Let’s find the square root of \(a = 16\) with an initial guess of \(x_0 = 1\) and an accepted error of \(0.1\).
| \(n\) | \(x_n\) | \(x_{n+1}\) | \(\epsilon\) |
|---|---|---|---|
| 0 | 1 | 8.5 | 0.88 |
| 1 | 8.5 | 5.04 | 0.69 |
| 2 | 5.04 | 4.0016 | 0.26 |
| 3 | 4.0016 | 3.999904 | 0.00004 |
After the third step, the error is less than the accepted error, so we stop iterating. The square root of \(16\) is \(4.0016\), which is close enough to the actual square root of \(16\) which is \(4\).
Implementation
The following code implements Newton’s method in Java:
public class NewtonsMethod {
public static double sqrt(double a, double x0, double epsilon) {
double x = x0;
double error = 1;
while (error > epsilon) {
double x1 = 0.5 * (x + a / x);
error = Math.abs(x1 - x) / x1;
x = x1;
}
return x;
}
}
Leetcode problem
We can use Newton’s method to solve the 69. Sqrt(x) problem on Leetcode.
class Solution {
public int mySqrt(int x) {
double x0 = 1;
double epsilon = 0.00000000000001;
double sqrt = NewtonsMethod.sqrt(x, x0, epsilon);
return (int) sqrt;
}
}
The same problem can be solved using binary search:
class Solution {
public int mySqrt(int x) {
long lo = 0, hi = x, mid, c;
while (lo <= hi) {
mid = (hi - lo) / 2 + lo;
c = mid * mid;
if (x == c) return (int)mid;
if(x > c) lo = mid + 1;
else hi = mid - 1;
}
return (int)hi;
}
}